 Количество движения
Количество движения
Количество движения материальной точки – векторная величина, равная произведению массы точки на вектор ее скорости.
Единицей измерения количества движения является (кг м/с).
Количество движения механической системы – векторная величина, равная геометрической сумме (главному вектору) количества движения механической системы равняется произведению массы всей системы на скорость ее центра масс.
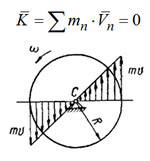
Когда тело (или система) движется так, что ее центр масс неподвижен, то количество движения тела равняется нулю (например, вращение тела вокруг неподвижной оси, проходящей через центр масс тела).
В случае сложного движения, количество движения системы не будет характеризовать вращательную часть движения при вращении вокруг центра масс. Т.е., количество движения характеризует только поступательное движение системы (вместе с центром масс).
Импульс силы
Импульс силы характеризует действие силы за некоторый промежуток времени.
Импульс силы за конечный промежуток времени определяется как интегральная сумма соответствующих элементарных импульсов.
Теорема об изменении количества движения материальной точки
(в дифференциальной форме):
Производная по времени от количества движения материальной точки равна геометрической сумме действующих на точки сил.
(в интегральной форме):
Изменение количества движения материальной точки за некоторый промежуток времени равняется геометрической сумме импульсов сил, приложенных к точке за этот промежуток времени.
Теорема об изменении количества движения механической системы
(в дифференциальной форме):
Производная по времени от количества движения системы равна геометрической сумме всех внешних сил, действующих на систему.
(в интегральной форме):
Изменение количества движения системы за некоторый промежуток времени равняется геометрической сумме импульсов внешних сил, действующих на систему за этот промежуток времени.
Теорема позволяет исключить из рассмотрения заведомо неизвестные внутренние силы.
Теорема об изменении количества движения механической системы и теорема о движении центра масс являются двумя разными формами одной теоремы.
Закон сохранения количества движения системы
- Если сумма всех внешних сил, действующих на систему, равна нулю, то вектор количества движения системы будет постоянным по направлению и по модулю.
- Если сумма проекций всех действующих внешних сил на любую произвольную ось равна нулю, то проекция количества движения на эту ось является величиной постоянной.
Выводы:
- Законы сохранения свидетельствуют, что внутренние силы не могут изменить суммарное количество движения системы.
- Теорема об изменении количества движения механической системы не характеризует вращательное движение механической системы, а только поступательное.
Приведен пример: Определить количество движения диска определенной массы, если известна его угловая скорость и размер.
Пример решения задачи на применение теоремы теоремы об изменении количества движения для определения скорости материальной точки