Изгибающий момент, поперечная сила и интенсивность распределенной нагрузки связаны следующими зависимостями (зависимостями Д.Н.Журавского):
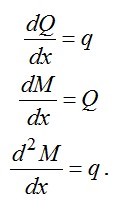
.
Выводы:
1 Если на некотором участке балки отсутствуюет распределенная нагрузка (q=0), то эпюра Q – прямая, параллельная к оси абсцисс (Q=const), а эпюра М на этом участке наклонная прямая.
2 Если на некотором участке есть равномерно распределенная нагрузка, то эпюра Q – наклонная прямая, параллельная оси абсцисс (Q=const), а эпюра М – парабола
3 Если на некотором участке балки:
Q > 0, то изгибающий момент возрастает,
Q < 0, то изгибающий момент убывает,
Q = 0, то изгибающий момент постоянный
4 Если поперечная сила, изменяясь по линейному закону, проходит через нулевое значение, то в соответствующем сечении изгибающий момент будет иметь экстремум.
5 Под сосредоточенной силой на эпюре Q образуется прыжок на величину приложенной силы, а на эпюру М – резкое изменение угла наклона соседних участков.
6 В сечении, где приложена пара сил, эпюра М будет иметь прыжок на величину момента пары. На эпюре Q это не отразиться.
7 Если равномерно распределенная нагрузка направлена вниз (вторая производная, которая характеризует кривизну линии), эпюра М обращена выпуклостью вверх, навстречу нагрузке.
Анализ построения эпюр с помощью дифференциальных зависимостей при изгибе.