 Общие принципы динамики
Общие принципы динамики
Принцип Германа – Эйлера - Даламбера
Сила инерции
Принцип Даламбера (принцип кинетостатики) является одним из общих принципов механики, с помощью которого уравнениям динамики по форме придается вид уравнений статики. Принцип был предложен Германом в 1716 году, обобщен Эйлером в 1737 году.
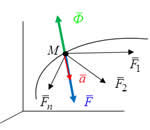
Материальная точка М движется с ускорением под действием приложенных сил. Третий закон динамики отображает двусторонность механических процессов природы. При взаимодействии двух тел приложенные к каждому из них силы равны по модулю и направлены противоположно. Так как эти силы приложены к разным телам, они не уравновешиваются. Например, при взаимодействия некоторого тела А и точки М, которая имеет массу m, точка получает ускорение. Тело А действует на точку М с силой F=-ma. По закону действия и противодействия материальное точка М действует на тело А с силой Ф=-F=-ma , которая называется силой инерции.
Сила инерции или сила Даламбера - векторная величина, имеющая размерность силы, по модулю равна произведению массы точки на ее ускорение, и направлена противоположно этому ускорению.
Принцип Даламбера для материальной точки
Если в любой момент времени к фактически действующим на материальную точку силам добавить силу инерции, то полученная система сил будет уравновешенной.
Это означает, что для решения задачи динамики по принципу Германа – Эйлера – Даламбера следует, помимо приложенных к точке сил, условно приложить к этой точке силу инерции . приложение силы инерции к точке является условным приемом, сводящим задачу динамики лишь по форме решения к задаче статики.
Принцип Даламбера для системы материальных точек
Если в любой момент времени к каждой из точек системы, кроме фактически действующих на нее внешних и внутренних сил, приложить соответствующие силы инерции, то полученная система сил будет находиться в равновесии и для нее можно будет применить все уравнения статики.
Принцип Даламбера для несвободной механической системы
В любой момент времени для каждой точки несвободной механической системы, кроме фактически действующих на нее сил, добавить соответствующие силы инерции, то полученная система сил будет уравновешенной и для нее можно будет применить все уравнения статики.
То есть, в любой момент времени для каждой точки несвободной механической системы геометрическая сумма главных векторов заданных сил, реакций опор и сил инерции материальных точек системы равна нулю.
В любой момент времени для любой точки несвободной механической системы геометрическая сумма главных моментов заданных сил, реакций опор и сил инерции материальных точек системы относительно любого неподвижного центра равна нулю.
Обобщенная форма уравнений равновесия по принципу Даламбера
Приведение сил инерции точек твердого тела к простейшему виду.
Случаи приведения системы сил инерции твердого тела простейшему виду.
Поступательное движение
При поступательном движении силы инерции твердого тела приводятся до одной равнодействующей, проходящей через центр масс тела, и равной по модулю произведению массы тела на модуль ускорения его центра масс и направленной противоположно этому ускорению.
Вращения вокруг центра масс нет, поэтому момент силы инерции равен нулю.
Вращательное движение тела вокруг оси, проходящей через центр масс тела.
Если тело вращается вокруг неподвижной оси проходящей через центр масс тела, то силы инерции приводятся к одной паре сил, лежащей в плоскости перпендикулярной оси вращения.
Поскольку центр масс не движется главный вектор сил инерции равен нулю.
Плоскопаралельний движение
При плоском движении тела система сил инерции приводится к силе, приложенной в центре масс тела и паре сил. Направление момента силы инерции противоположен угловому ускорению тела.
Принцип возможных перемещений
Принцип возможных перемещений в общем виде определяет условия равновесия любой механической системы, то есть позволяет решать задачи статики, как задачи динамики.
Перемещение точек несвободной механической системы ограничено имеющимися связями. Положение точек системы определяется заданием независимых координат.
Независимые величины, заданием которых можно однозначно определяется положение всех точек механической системы, называются обобщенными координатами этой системы. Как правило, число обобщенных координат механической системы равно числу степеней свободы этой системы. Например, положение всех точек кривошипно-шатунного механизма определяется заданием угла поворота кривошипа.
Возможные или виртуальные перемещения
Возможные или виртуальные перемещения системы – это воображаемые бесконечно малые перемещения точек системы, допускаемые в данный момент наложенными на систему связями.
Криволинейные перемещения точек заменяют прямолинейными отрезками, отложенными по касательной к траекториям точек.
Число независимых между собой возможных перемещений системы называется числом степеней свободы этой системы.
Возможная или виртуальная работа
Возможная (или виртуальная) работа − это элементарная работа, которую действующая на материальную точку сила могла бы совершить на перемещении, совпадающем с возможным перемещением этой точки.
Принцип возможных перемещений для механической системы
Для равновесия механической системы с идеальными связями необходимо и достаточно, чтобы сумма робот всех активных сил при любом возможном перемещении системы равнялась нулю.
Уравнение возможных работ − математическое выражение необходимого и достаточного условий равновесия любой механической системы.
Общее уравнение динамики
Общее уравнение динамики (принцип Даламбера – Лагранжа)
Принцип возможных перемещений, дающий общий метод решения задач статики, можно применить и к решению задач динамики. На основании принципа Германа—Эйлера—Даламбера для несвободной механической системы в любой момент времени геометрическая сумма равнодействующей задаваемых сил, равнодействующей реакций связей и силы инерции для каждой точки Mn механической системы равна нулю.
Если система получает возможное перемещение, при котором каждая точка имеет возможное перемещение , то сумма работ этих сил на перемещении должна быть равна нулю.
Общее уравнение динамики для системы с идеальными связями
Положим, что все связи в рассматриваемой механической системе двусторонние и идеальные (силы трения, если они имеются, отнесены к числу задаваемых сил). Тогда сумма работ реакций связей на возможных перемещениях системы равна нулю.
При движении механической системы с идеальными связями в любой данный момент времени сумма элементарных робот всех активных (заданных) сил и всех сил инерции на любом возможном перемещении системы равняется нулю.
Общие уравнения динамики позволяют составить дифференциальные уравнения движения любой механической системы. Если механическая система состоит из отдельных твердых тел, то силы инерции точек каждого тела можно привести к силе, приложенной в некоторой точке тела, и паре сил. Сила равна главному вектору сил инерции точек этого тела, а момент пары равен главному моменту этих сил относительно центра приведения. Чтобы воспользоваться принципом возможных перемещений, к каждому телу прикладывают действующие на него задаваемые силы, а также условно прикладывают силу и пару, составленные силами инерции точек тела. Затем системе сообщают возможное перемещение и для всей совокупности задаваемых сил и приведенных сил инерции составляют общее уравнение динамики
Формат: pdf
Размер: 600КВ
Язык: русский, украинский
Пример решения задачи