Обзор
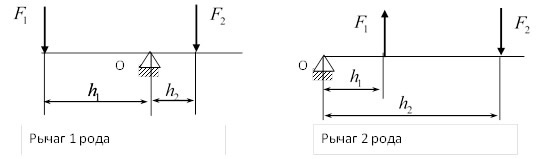
Рычаг – это твердое тело, имеющее недвижимую ось вращения и находящееся под действием сил, лежащих в плоскости, перпендикулярной этой оси.
Если рычаг находится в состоянии покоя, то алгебраическая сумма моментов всех сил, приложенных к рычагу относительно опорной точки, равняется нулю
Произвольная плоская система сил – это система сил, линии действия которых расположены в плоскости независимо.
Методом Пуансо в центре приведения О будет получена система сил и система пар, моменты каждой из которых равняют моментам соответствующей силы относительно центра приведения.
Главным вектором системы называется вектор, который равняется геометрической сумме всех сил системы.
Главным моментом системы относительно центра О в плоскости называется алгебраическая сумма моментов сил системы относительно центра приведения О.
Главный вектор не зависит от выбора центра приведения О. Главный момент сил зависит от центра приведения.
Основная теорема статики о приведении системы сил к данному центру: Какая-либо плоская произвольная система сил, действующих на абсолютно твердое тело, при приведении к произвольно избранному центру О, может быть заменена одной силой , равняющейся главному вектору системы и приложенной в центре приведения О, и одной парой с моментом , равняющемуся главному моменту системы относительно центра О.
Рассмотрены случаи приведения плоской системы сил к более простому виду
Условия равновесия произвольной плоской системы сил.
1. Геометрические условия равновесия: для равновесия плоской произвольной системы сил необходимо и достаточно, чтобы главный вектор и главный момент системы равнялись нулю
2. Аналитические условия равновесия.
Основная форма условий равновесия: Для равновесия произвольной плоской системы сил необходимо и достаточно, чтобы суммы проекций всех сил на координатные оси и сумма их моментов относительно любого центра, который лежит в плоскости действия сил, равнялись нулю.
Вторая форма условий равновесия: Для равновесия произвольной плоской системы сил необходимо и достаточно, чтобы суммы моментов всех сил относительно любых двух центров А и В и сумма их проекций на ось, не перпендикулярную прямой АВ, равнялись нулю.
Третья форма условий равновесия (уравнение трех моментов): Для равновесия плоской произвольной системы сил необходимо и достаточно, чтобы суммы моментов всех сил относительно любых трех центров А, В и С, не лежащих на одной прямой, равнялись нулю.
Центр параллельных сил
Система параллельных сил, направленных в одну сторону, не может быть уравновешена или приводиться к паре сил, она всегда имеет равнодействующую.
Линия действия равнодействующей параллельна силам. Положение точки ее приложение зависит от величин и положения точек приложения сил системы.
Центр параллельных сил – точка С точка приложения равнодействующей системы параллельных сил.
Положение центра параллельных сил – точки С, определяется координатами этой точки
Центр тяжести твердого тела и его координаты
Центр тяжести тела - неизменно связанная с этим телом геометрическая точка, в которой приложена равнодействующая сил тяжести отдельных частиц тела, т.е. вес тела в пространстве.
Координаты центра тяжести определяются аналогично координатам центра параллельных сил С ( ), составленных силами тяжести частиц тела.
Положение центра тяжести однородного тела зависит только от его геометрической формы и размеров, и не зависит от свойств материала, из которого тело выполнено.
Сумма произведений элементарных площадей, входящих в состав плоской фигуры, на алгебраические значения их расстояний до некоторой оси, называется статическим моментом площади плоской фигуры.
Статический момент площади плоской фигуры равняется произведению площади фигуры на алгебраическое расстояние от центра тяжести до этой оси. Единица измерения статического момента [см3].
статический момент площади плоской фигуры относительно оси, которая проходит через центр тяжести фигуры, равняется нулю.
Вес тела это равнодействующая сил тяжести отдельных частиц тела.
Способы определения положения центра тяжести.
- Метод симметрии: Если однородное тело имеет плоскость, ось или центр симметрии, то центр тяжести лежит соответственно или в плоскости симметрии, или на оси симметрии, или в центре симметрии.Центр тяжести линии длиной - по середине. Центр тяжести окружности (или круга) радиуса - в его центре, т.е. в точке пересечения диаметров. Центр тяжести параллелограмма, ромба или параллелепипеда – в точке пересечения диагоналей. Центр тяжести правильного многоугольника - в центре вписанного или описанный круга.
- Метод разбивки: Если тело можно разбить на конечное количество элементов (объемов, плоскостей, линий), для каждой из которых положение центра тяжести известно, то координаты центра тяжести всего тела можно определить зная значения для элементов непосредственно по формулам
- Метод дополнения (отрицательных плоскостей): Если тело имеет вырезанные элементы, то при разбивке на элементы, вырезанная часть (площадь, объем) отнимаются из общей, т.е. вырезанным элементам даются отрицательные значения площади или объема
Произвольная пространственная система сил
Формат: pdf
Размер: 700 КВ
Язык: русский, украинский