 Лекция 2. Колебательное движение материальной точки
Лекция 2. Колебательное движение материальной точки
Общие сведения
Колебательное движение материальной точки происходит в случае, когда на точку, отклоненную от состояния покоя, действует сила, старающаяся возвратить точку в исходное положения.
Сила, старающаяся возвратить материальную точку в положение равновесия, называется восстанавливающей силой.
Колебательным движением называется движение, которое характеризуется многократным прохождением положения равновесия.
Виды колебательного движения материальной точки:
- свободные колебания, создающиеся только под действием восстанавливающей силы;
- затухающие колебания − свободные колебания, создающиеся под действием восстанавливающей силы и силы сопротивления среды;
- вынужденные колебания, создающиеся под действием восстанавливающей силы и силы периодического характера, называемой возмущающей силой;
- вынужденные колебания, создающиеся под действием восстанавливающей силы, возмущающей силы и силы сопротивления среды.
Свободные колебания материальной точки
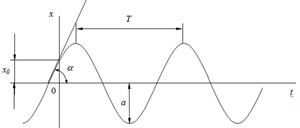
Период колебаний Т – промежуток времени, за который происходит одно полное колебание.
Амплитуда колебаний – величина, равная наибольшему отклонению точки от центра колебаний.
Начальная фаза – определяет фазу начала колебаний, которая соответствует начальным условиям.
Вывод:
- Амплитуда свободных колебаний величина постоянная.
- Частота и период свободных колебаний материальной точки зависят только от массы точки m и коэффициента с, характеризующего восстанавливающую силу, и не зависят от начальных условий движения.
Затухающие колебания материальной точки
Свободные колебания материальной точки представляют собой идеальный случай. Материальная точка, совершающая колебательное движение в реальных условиях, ощущает сопротивление движению, то есть, находится под действием не только восстанавливающей силы, направленной к центру колебаний, но и силы сопротивления, которая всегда направлена в сторону противоположную направлению движения точки.
Сила сопротивления пропорциональна скорости движения точки.
Амплитуда затухающих колебаний – наибольшее отклонение точки от положения равновесия за время каждого колебания.
При отсутствии сопротивления материальная точка совершает свободные колебания.
В случае большого сопротивления движение материальной точки теряет колебательный характер и приводится к апериодическому движению.
Вслучае предельного сопротивления движение точки теряет колебательный характер. Со временем график движения асимптотически приближается к положению равновесия.
Вынужденные колебания
Вынужденные колебания материальной точки при отсутствии сопротивления.
Вынужденные колебания материальная точка совершает, когда на нее, наряду с восстанавливающей силой, действует возмущающая сила, периодически меняющаяся со временем.
Вывод:
- При одновременном действии восстанавливающей и возмущающей сил материальная точка совершает сложное колебательное движение, которое является результатом наложения свободных и вынужденных колебаний.
- Вынужденные колебания не зависят от начальных условий движения материальной точки.
Вынужденные колебания материальной точки под влиянием сопротивления (вынужденные затухающие колебания)
На материальную точку наряду с восстанавливающей и возмущающей силой, действует сила сопротивления.
Общее решение дифференциального уравнения зависит от соотношения коэффициента затухания и частоты свободных колебаний.
При одновременном действии восстанавливающей силы, возмущающей силы и силы сопротивления материальная точка соверщает сложное колебательное движение, которое является наложением затухающих и вынужденных колебаний.
Явление резонанса возникает при совпадении частот вынужденных и свободных колебаний . Амплитуда колебаний при резонансе возрастает пропорционально времени до бесконечности.
Вывод:
- Амплитуда вынужденных колебаний не зависит от начальных условий.
- Вынужденные колебания не угасают при наличии сопротивления.
- Частота вынужденных колебаний равна частоте возмущающей силы и не зависит от характеристик колебательной системы.
- Даже при малой возмущающей силе можно получить интенсивные вынужденные колебания, если сопротивление мало, а частота р близка к k (резонанс).
- Даже при больших значениях возмущающей силы можно создать довольно малые вынужденные колебания, если частота р будет значительно больше, чем k.
- Влияние сопротивления на вынужденные колебания проявляются в смещении фазы колебаний по отношению к фазе возмущающей силы и в уменьшении амплитуды колебаний по мере увеличения сопротивления.
Формат: pdf
Язык: русский, украинский
Размер: 700 КВ
Лекция 1. Динамика точки