Какое-либо кинематич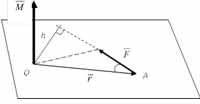еское состояние тел, имеющих точку или ось вращения, можно описать моментом силы, характеризующим вращательный эффект действия силы. Момент силы относительно центра - это векторное произведение радиус – вектора точки приложения силы на вектор силы.

Теоремы о паре сил
        Теорема 1. Пара сил не имеет равнодействующей, т.е. пару сил нельзя
заменить одной силой.
       Теорема 2. Пара сил не является системой уравновешенных сил.
Следствие: пара сил, действующая на абсолютно твердое тело,
старается вращать его.
       Теорема 3. Сумма моментов сил пары относительно произвольного
центра (точки) в пространстве является величиной неизменной и
представляет собой вектор-момент этой пары.

   Пара сил – система двух параллельных, равных по модулю и противоположных по направлению сил, приложенных к абсолютно твердому телу.
   Плечо пары сил h – расстояние между линиями действия сил пары, т.е. длина перпендикуляра, проведенного из произвольной точки линии действия одной из сил пары на линию действия второй силы.
   Плоскость действия пары сил – это плоскость, в которой расположены линии действий сил пары.
Действие пары сил сводится к вращательному движению, которое определяется моментом пары.
Моментом пары называется вектор с такими признаками:
- он перпендикулярен плоскости пары;
- направлен в ту сторону, откуда
вращение, которое осуществляет пара,
видно против часовой стрелки;
- его модуль равняется произведению
модуля одной из сил пары на плечо h

Содержание

1. Момент силы относительно центра в плоскости
2. Свойства момента силы относительно центра
3. Теорема Вариньона
4. Сложение двух параллельных сил, направленных в одну сторону
5. Сложение двух параллельных сил, направленных в разные стороны
6. Пары сил
7. Момент пары
8. Теоремы о паре сил
9. Условия равновесия системы пар сил

Язык: русский, украинский

Размер: 266 KВ

Пример решения задачи