 Теорема о движении центра масс механической системы
Теорема о движении центра масс механической системы
Масса системы равняется алгебраической сумме масс всех точек или тел системы.
В однородном поле тяжести, для которого , вес любой частицы тела пропорционален его массе. Поэтому распределение масс в теле можно определить по положению его центра тяжести – геометрической точки, называемой центром масс или центром инерции механической системы
Теорема: центр масс механической системы движется как материальная точка, масса которой равна массе системы, к которой приложены все внешние силы, действующие на систему.
Выводы:
Механическую систему или твердое тело можно рассматривать как материальную точку в зависимости от характера ее движения, а не от ее размеров.
Внутренние силы не учитываются теоремой о движении центра масс.
Теорема о движении центра масс не характеризует вращательное движение механической системы, а только поступательное.
Теорема об изменении количества движения
Количество движения материальной точки – векторная величина, равная произведению массы точки на вектор ее скорости.
Количество движения механической системы – векторная величина, равная геометрической сумме (главному вектору) количества движения всех точек системы или количество движения системы равняется произведению массы всей системы на скорость ее центра масс.
Когда тело (или система) движется так, что ее центр масс остается неподвижным, то количество движения тела равно нулю (например, вращение тела вокруг неподвижной оси, проходящей через центр масс тела).
Если движение тела сложное, то количество движения не будет характеризовать вращательную часть движения при вращении вокруг центра масс. Т.е., количество движения характеризует только поступательное движение системы (вместе с центром масс).
Импульс силы характеризует действие силы за некоторый промежуток времени.
Импульс силы за конечный промежуток времени определяется как интегральная сумма соответствующих элементарных импульсов
Теорема об изменении количества движения материальной точки (в дифференциальной форме):
Производная по времени от количества движения материальной точки равна геометрической сумме действующих на точку сил.
Теорема об изменении количества движения материальной точки (в интегральной форме):
Изменение количества движения материальной точки за некоторый промежуток времени равняется геометрической сумме импульсов сил, приложенных к точке за этот промежуток времени.
Теорема об изменении количества движения механической системы (в дифференциальной форме):
Производная по времени от количества движения системы равна геометрической сумме всех действующих на систему внешних сил.
Теорема об изменении количества движения механической системы (в интегральной форме):
Изменение количества движения системы за некоторый промежуток времени равняется геометрической сумме импульсов внешних сил, действующих на систему, за тот же промежуток времени.
Закон сохранения количества движения системы.
- Если сумма всех внешних сил, действующих на систему, равняется нулю, то вектор количества движения системы будет постоянным по направлению и по модулю.
- Если сумма проекций всех действующих внешних сил на какую-нибудь произвольную ось равна нулю, то проекция количества движения на эту ось является величиной постоянной.
Законы сохранения свидетельствуют, что внутренние силы не могут изменить суммарное количество движения системы.
Теорема об изменении момента количества движения
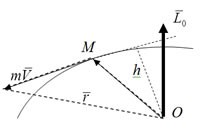
Момент количества движения точки М относительно центра О − это вектор, направленный перпендикулярно плоскости, проходящей через вектор количества движения и центр О в ту сторону, откуда поворот вектора количества движения относительно центра О виден против часовой стрелки.
Момент количества движения точки М относительно оси равняется произведению проекции вектора количества движения на плоскость перпендикулярную оси , на плечо этой проекции относительно точки О пересечения оси с плоскостью.
Теорема (относительно центра)
Производная по времени от момента количества движения материальной точки относительно некоторого неподвижного центра равняется геометрической сумме моментов сил, действующих на точку, относительно того же центра.
Теорема (относительно оси).
Производная по времени от момента количества движения материальной точки относительно некоторой неподвижной оси равняется алгебраической сумме моментов сил, действующих на точку, относительно этой же оси.
Законы сохранения момента количества движения.
- Если линия действия равнодействующей приложенных к материальной точке сил все время проходит через некоторый неподвижный центр, то момент количества движения материальной точки остается постоянным.
- Если момент равнодействующей приложенных к материальной точке сил относительно некоторой оси все время равняется нулю, то момент количества движения материальной точки относительно этой же оси остается постоянным.
Кинетическим моментом или главным моментом количества движения механической системы относительно центра называют вектор, который равняется геометрической сумме моментов количества движения всех материальных точек системы относительно этого же центра.
Кинетическим моментом или главным моментом количеств движения механической системы относительно оси называют алгебраическую сумму моментов количеств движения всех материальных точек относительно той же оси
Проекция кинетического момента механической системы относительно центра О на ось, проходящую через этот центр, равняется кинетическому моменту системы относительно этой оси.
Теорема об изменении главного момента количества движения системы (относительно центра) – теорема моментов.
Производная по времени от кинетического момента механической системы относительно некоторого неподвижного центра геометрически равняется главному моменту внешних сил, действующих на эту систему, относительно того же центра.
Теорема об изменении кинетического момента механической системы (относительно оси).
Производная по времени от кинетического момента механической системы относительно некоторой оси равняется главному моменту внешних сил относительно этой же оси.
Теорема моментов имеет большое значение при изучении вращательного движения тел и разрешает не учитывать заведомо неизвестные внутренние силы.
Законы сохранения кинетического момента механической системы.
- Если главный момент внешних сил относительно некоторого неподвижного центра все время равняется нулю, то кинетический момент механической системы относительно этого центра величина постоянная.
- Если главный момент внешних сил относительно некоторой оси равняется нулю, то кинетический момент механической системы относительно этой же оси величина постоянная.
Внутренние силы не могут изменить главный момент количества движения системы.
Случай вращающейся системы.
Для вращающейся вокруг неподвижной оси (или оси, проходящей через центр масс) системы, кинетический момент относительно оси вращения равняется произведению момента инерции относительно этой оси на угловую скорость.
Теорема об изменении кинетической энергии.
Кинетическая энергия это способность тела преодолевать препятствование во время движения.
Кинетической энергией материальной точки называется скалярная величина, равная половине произведения массы точки на квадрат ее скорости.
Кинетическая энергия:
- характеризует и поступательное и вращательное движения;
- не зависит от направления движения точек системы и не характеризует изменение этих направлений;
- характеризует действие и внутренних, и внешних сил.
Кинетическая энергия системы равняется сумме кинетических энергий тел составляющих систему. Кинетическая энергия зависит от вида движения тел системы.
Теорема Кьонига (о кинетической энергии системы):
Кинетическая энергия механической системы равняется сумме кинетической энергии центра масс системы, масса которого равна массе системы, и кинетической энергии системы в ее относительном движении относительно центра масс.
Кинетическая энергия зависит от вида движения тел системы.
Определение кинетической энергии твердого тела при разных видах движения движениях.
Работа силы.
Работа силы характеризует действие силы на тело при некотором перемещении и определяет изменение модуля скорости подвижной точки.
Элементарная работа силы определяется как скалярная величина , равная произведению проекции силы на касательную к траектории, направленную в направлении движения точки, на бесконечно малое перемещение точки, направленное вдоль этой касательной
Мощность – это величина, определяющая работу силы за единицу времени.
Случаи определения работы сил.
- Работа силы тяжести.
- Работа силы упругости.
- Работа силы трения
- Работа сил, приложенных к вращающемуся телу.
Теорема об изменении кинетической энергии материальной точки:
Изменение кинетической энергии материальной точки на некотором ее перемещении равняется алгебраической сумме робот всех действующих на точку сил на этом же перемещении.
Теорема об изменении кинетической энергии механической системы:
Изменение кинетической энергии механической системы на некотором перемещении равняется алгебраической сумме робот внутренних и внешних сил, действующих на материальные точки системы на том же перемещении.
Теорема об изменении кинетической энергии неизменной механической системы:
Изменение кинетической энергии неизменной системы на некотором перемещении равняется сумме робот внешних сил, действующих на точки системы на том же перемещении.
Размер: 420КВ