Плоскопараллельное движение
 Плоскопараллельным или плоским движением твердого тела называется движение, при котором все точки тела движутся в плоскостях, которые параллельны некоторой недвижимой плоскости (базовой).
Плоскопараллельным или плоским движением твердого тела называется движение, при котором все точки тела движутся в плоскостях, которые параллельны некоторой недвижимой плоскости (базовой).
Изучение плоского движения абсолютно твердого тела сведится к изучению одного сечения плоской фигуры, которое определяется движением трех точек, которые не лежат на одной прямой.
Задав угол поворота тела вокруг прямой, которая проходит через полюс А перпендикулярно к плоскости сечения, получим закон плоскопаралельного движения
Плоскопараллельное движение твердого тела состоит из поступательного,при котором точки тела движутся вместе с полюсом, и вращательного вокруг полюса.
Основные кинематические характеристики плоского движения тела:
- скорость и ускорение поступательного движения полюса,
- угловая скорость и угловое ускорение вращательного движения вокруг полюса.
Траектория произвольной точки плоской фигуры определяется расстоянием от точки до полюса А и углом вращения вокруг полюса.
Определение скоростей точек плоской фигуры
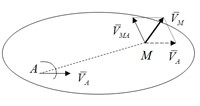
Скорость произвольной точки равна геометрической сумме скорости точки, которая принята за полюс, и вращательной скорости данной точки в ее вращательном движении вместе с телом вокруг полюса.
Модуль и направление скорости находится построением соответствующего параллелограмма.
Мгновенный центр скоростей (МЦС)
Мгновенный центр скоростей (МЦС ) - точка, скорость которой в данный момент времени равна нулю. МЦС рассматривают в качестве полюса.
- Скорость произвольной точки тела, которая принадлежит плоской фигуре, равняется ее вращательной скорости вокруг мгновенного центра скоростей. Модуль скорости произвольной точки А равняется произведению угловой скорости тела на длину отрезка от точки до МЦС. Вектор направлен перпендикулярно к отрезку от точки до МЦС в направлении вращения тела
- Модули скоростей точек тела пропорциональны их расстояниям до МЦС
Случаи определения мгновенного центра скоростей
- Если известны скорость одной точки тела, угловая скорость вращения тела, то для нахождения МЦС (Р) необходимо повернуть вектор скорости точки в сторону вращения на 900 и на найденном луче отложить отрезок АР
- Если скорости двух точек тела параллельны и перпендикулярны прямой, которая проходит через эти точки, то МЦС находится в точке пересечения этой прямой и прямой, которая соединяет концы векторов скоростей
- Если известны направления скоростей двух точек тела и их направления не параллельны, то МЦС находится в точке Р пересечения перпендикуляров, проведенных к скоростям в этих точках
- Если колесо катится по недвижимой поверхности без скольжения, то МЦС (Р) находится в точке соприкосновения колеса с недвижимой поверхностью
В случаях 2 и 3 возможные исключения (мгновенно поступательное движение или мгновенный покой).
Плоскопараллельное движение можно считать сложным движением
Сложное движение точки
Сложное движение точки - движение, при котором точка одновременно принимает участие в нескольких движениях.
Относительное движение - движение относительно подвижной системы отсчета.
Переносное движение - движениет подвижной системы отчета (переносящей среды) вместе с точкой относительно неподвижной системы отсчета.
Абсолютное движение - движение точки относительно недвижимой системы отсчета
Абсолютное движение точки является сложным движением, т.к. состоит из относительного и переносного движений.
При сложном движении абсолютная скорость точки равняется геометрической сумме ее относительной и переносной скоростей
Определение ускорений точки
Абсолютное ускорение точки равняется геометрической сумме трех векторов: относительного ускорения, характеризующего изменение относительной скорости в относительном движении; переносного ускорения, характеризующего изменение переносной скорости точки в переносном движении, и ускорения Кориолиса, характеризующего изменение относительной скорости точки в переносном движении и переносной скорости в относительном движении.
Ускорением Кориолиса точки называется двойное векторное произведение угловой скорости переносящей среды и относительной скорости точки.
Формат: pdf
Размер:
Язык: русский, украинский