 Поступательное движение твердого тела
Поступательное движение твердого тела
Поступательным называется такое движение твердого тела, при котором любая прямая перемещается параллельно сасой себе.
При поступательном движении:
- траектории всех точек тела одинаковы ;
- скорости всех точек тела в данный момент времени ;
- ускорение всех точек тела в данный момент времени одинаковы;
Поступательное движение тела определяется движением любой одной его точки, т.е. кинематика поступательного движения сводится к кинематике точки.
Вращательное движение твердого тела
Вращательным движением твердого тела называется такое движение, при котором существуют неподвижные точки, лежащие на прямой, называемой осью вращения.
Все другие точки тела движутся в плоскостях, перпендикулярных оси вращения и описывают окружности, радиусы которых равняются расстояниям от точек до оси вращения, а центры лежат на неподвижной оси.
Угол поворота - двугранный угол, который образуется при вращении тела, между подвижной и неподвижной полуплоскостями.
Каждому моменту времени соответствует определенное значение угла поворота, т.е. угол является функцией времени и представляет собой закон вращательного движения.
Единицей измерения угла вращения является 1 радиан.
Угловая скорость − вектор, направленный вдоль оси вращения в ту сторону, откуда вращения тела видно против движения часовой стрелки и проекция которого на ось вращения равняется первой производной от угла поворота по времени.
Угловая скорость определяет направление вращения тела.
Единицы измерения угловой скорости 1 (рад/сек) или (с -1) .
Угловое ускорение − вектор, направленный вдоль оси вращения и его проекция на ось вращения равняется первой производной от угловой скорости по времени или второй производной от угла поворота по времени.
Векторы и не имеют точки приложения, являются скользящими условными векторами.
Вращение тела считается:
- ускоренным, если модуль угловой скорости с течением времени возрастает, т.е. величины и совпадают по знаку
- замедленным, если модуль угловой скорости с течением времени уменьшается, т.е. величины и противоположные по знаку
- равномерным, если – угловая скорость тела постоянна
Единица измерения углового ускорения 1 (рад/сек -2) или 1 (с -2).
Угловая скорость и угловое ускорение – кинематические характеристики всего тела.
Скорость точки твердого тела, вращающегося вокруг неподвижной оси называют линейной или окружной скоростью.
Линейная (окружная) скорость точки зависит от угловой скорости тела и радиуса вращения .
Вектор линейной скорости направлен по касательной к траектории – окружности вращения.
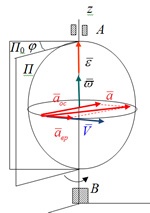
Ускорения точки твердого тела, вращающегося вокруг неподвижной оси
Линейное ускорение точки тела при вращении складывается из вращательного и осестремительного ускорения, составляющих полное ускорение .
Вращательное ускорение (касательное) ускорение зависит от алгебраической величины углового ускорения тела и радиуса вращения.
Вектор вращательного ускорения направлен по касательной к окружности коллинеарно вектору скорости.
Осестремительное ускорение (нормальное) ускорение точки зависит от угловой скорости вращения тела и радиуса вращения
Вектор осестремительного ускорения направлен по радиусу вращения точки к центру вращения.
Полное ускорение точки тела пределяют, как векторную сумму вращательного и осестремительного ускорений.
Кинематика зубчатых механизмов
Механизм - система тел, предназначенная для преобразования движения одного или нескольких тел в необходимые движения других тел.
Передаточный механизм служит для преобразования вида движения, изменения величины и направления скорости рабочего органа.
Зубчатые механизмы – механизмы, в которых передача движения от одного звена к другому происходит по помощи зубьев, нанесенных на поверхность звена.
Они получили широкое использование в технике: кинематических передачах, приборах и т.п.
Профиль зубьев зубчатых колес чаще всего эвольвентный. Эвольвента – траектория точки, лежащей на прямой, которая может быть получена в результате перекатывания прямой по окружности без скольжения.
Основная теорема зацепления - теорема Виллиса
Зацепление зубьев зубчатых колес будет непрерывным с постоянным передаточным отношением, если общая нормаль к боковым профилям зубьев делит межосевое расстояние на части обратно пропорциональные угловым скоростям, а точка пересечения общей нормали с линией центров занимает постоянное положение.
Полюс зацепления (Р) – точка пересечения общей нормали с линией центров.
Окружности, проходящие через полюс зацепления, называются основными окружностями. В процессе вращения зубчатых колес эти окружности перекатываются друг по другу без скольжения. В передачах, изготовленных без смещения режущего инструмента, основные окружности совпадают с делительными. Общая нормаль n-n имеет название линия зацепления, все точки контакта зубьев всегда находятся на этой линии.
Угол между общей нормалью и общей касательной называется угол зацепления .
С помощью одной пары зубчатых колес возможно реализовать передаточное отношение до 6. Если надо реализовать большее передаточное отношение используют сложные зубчатые механизмы:
- механизмы с недвижимыми осями;
- механизмы, в которых некоторые оси вращаются вокруг неподвижных осей (сателитные).
Механизмы с неподвижными осями:
Ступенчатое зацепление – колеса находятся в зацеплении попарно (стрелочный электропривод).
Общее передаточное отношение ступенчатого механизма равняется произведению передаточных отношений отдельных степеней, или отношению произведения чисел зубьев парных зубчатых колес к произведению чисел зубьев непарных зубчатых колес.
Знак передаточного отношения:
- для внешнего зацепления –
- для внутреннего зацепления +
Когда количество внешних зацеплений нечетное знак «−», когда четное «+».
Рядное зацепление – общее передаточное отношение равняется произведению передаточных чисел отдельных степеней.
Общее передаточное отношение рядового зацепления зависит от количества зубьев крайних механизмов. Промежуточные зубчатые колеса, не влияющие на передаточное отношение, называются паразитарными
Формат: pdf.
Язык: русский, украинский.
Размер: 430КВ