Сдвиг

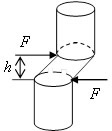
 Сдвиг – такой вид деформации, при котором одно сечение стержня смещается относительно другого, а расстояние между ними не изменяется.

 Сдвиг может быть вызван действием двух равных, параллельных и противоположно направленных сил, расположенных на  близком расстоянии друг от друга перпендикулярно к оси стрежня.

 Детали, служащие для соединения элементов металлоконструкций, механизмов и машин (заклепки, болты, булавки, сварные швы и т.п.), воспринимают нагрузки, перпендикулярные их продольной оси, т.е. испытывают сдвиг.

 Во внутреннем сечении при сдвиге возникает  один силовой фактор – перерезывающая сила Q.

 Касательные напряжения лежат в плоскости сечения. В случае недостаточной прочности  происходит перерезывание деталей. Говорят, что детали работают на срез, и касательные напряжения называют напряжениями среза.

 При сдвиге одна плоскость смещается относительно другой. Степень смещения характеризуется абсолютным сдвигом, зависящим от расстояния h между сечениями. Во избежание влияния h, вводят понятие относительного сдвига.

 Относительный сдвиг равняется угловому перемещению продольного волокна элемента – углу сдвига.

 Между углом сдвига и касательным напряжения  существует прямая пропорциональность – закон Гука при сдвиге, G – упругая постоянная материала, модуль сдвига (модуль Юнга второго рода).

 Между модулем продольной упругости Е и модулем сдвига G имеется зависимость

Геометрические характеристики сечений

1. Площадь поперечного сечения (при растяжении, сжатии).
2. Статические моменты сечения относительно осей Х и Y ([м3]). Если оси координат проходят через центр тяжести сечения, то статические моменты равны нулю. Оси называются центральными.
3. Координаты центра тяжести
4. Моменты инерции [м4]:

• осевые
• центробежный
• полярный

  Оси, относительно которых центробежный момент инерции равняется нулю, называются главными осями инерции. Осевые моменты инерции относительно главных осей координат принимают экстремальные значения.

Кручение

  Кручение имеет место при нагрузке вала внешними силами, плоскости действия которых перпендикулярны  его продольной оси (вал со шкивами, зубчатыми колесами и т.п.). Моменты этих сил - вращающие моменты.

 При кручении в поперечном сечении возникает внутренний силовой фактор – крутящий момент Т. На основании метода сечений, крутящий момент в сечении равняется алгебраической сумме внешних скручивающих моментов, действующих с одного стороны рассматриваемого сечения.

 При приложении крутящего момента Т к концу жестко закрепленного вала образующая ab повернется на угол сдвига при кручении.

 Поперечные сечения поворачиваются относительно друг друга на некоторый угол − угол закручивания.

Формат: pdf

Язык: русский, украинский

Размер: 430КВ

Пример решения задачи на кручение