Обзор

Основными задачами в технике являются обеспечения прочности, жесткости, устойчивости инженерных конструкций, деталей машин и приборов.

 Наука, в которой изучаются  принципы и методы расчетов на прочность, жесткость и устойчивость называется сопротивлением материалов.

 Прочность – это способность конструкции в определенных пределах воспринимать действие внешних нагрузок без разрушения.

 Жесткость – это способность конструкции в определенных пределах воспринимать действие внешних нагрузок без  изменения геометрических размеров (не деформируясь).

 Устойчивость – свойство системы самостоятельно восстанавливать первоначальное состояние после того, как ей было дано некоторое отклонение от состояния равновесия.

 Каждый инженерных расчет состоит из трех этапов:

1. Идеализация объекта (выделяются наиболее существенные особенности реальной конструкции - создается расчетная схема).
2. Анализ расчетной схемы.
3. Обратный переход от расчетной схемы к реальной конструкции и формулирование выводов.

 Сопротивление материалов базируется на  законах теоретической механики (статика), методах математического анализа, материаловедении.

Классификация нагрузок

 Различают внешние и внутренние силы и моменты. Внешние силы (нагрузки) – это активные силы и реакции связи.

 По характеру действия  нагрузки делятся на:

• статические – прикладывается медленно, возрастая от нуля до конечного значения, и не изменяются;
• динамические – изменяют величину или направление  за короткий промежуток времени:
  • внезапные - действуют сразу на полную силу (колесо локомотива, заезжающего  на мост),
  • ударные – действуют на протяжении короткого времени (дизель-молот),
  • циклические (нагрузка на зубья зубчатого колеса).

Классификация элементов конструкций

 Стержень (брус) – тело, длина которого  L превышает его поперечные размеры b и h. Ось стержня – линия, соединяющая центры тяжести последовательно расположенных сечений. Сечение – это плоскость перпендикулярная  оси стрежня.

 Пластина – тело плоской формы, у которого длина a и ширина b больше по сравнению с толщиной h.

 Оболочка – тело, ограниченное двумя близко расположенными криволинейными поверхностями. Толщина оболочки мала по сравнению с другими габаритными размерами, радиусами кривизны ее поверхности.

 Массивное тело (массив) – тело, у которого все размеры одного порядка.

Деформации стержня

 При нагрузке тел внешними силами они могут изменять свою форму и размеры. Изменение формы и размеров тела под действием внешних сил называется деформацией.

Деформации бывают:

• упругие - исчезают после прекращения действия вызвавших их сил;
• пластичные - не исчезают после прекращения действия вызвавших их сил.

  В зависимости  от характера внешних нагрузок различают такие виды деформаций:

• растяжение-сжатие – состояние сопротивления, которое характеризуется удлинением или укорочением,
• сдвиг – смещение двух сопредельных поверхностей относительно друг друга при неизменном расстоянии между ними,
• кручение – взаимный поворот поперечных сечений относительно друг друга,
• изгиб – состоит в искривлении оси.

  Бывают более сложные деформации, которые образуются сочетанием нескольких основных.

 Линейные деформации связаны с перемещением точек или сечений вдоль прямой линии (растяжение, сжатие).

 Угловые деформации связаны с относительным поворотом одного сечения относительно другого (кручение).

Основные гипотезы и принципы

 Гипотеза о сплошности материала: тело, сплошное и непрерывное до деформации, остается таким же и  в процессе деформации.

 Гипотеза об однородности и изотропности: в любой точке тела и в любом направлении физико-механические свойства материала считаются одинаковыми.

 Гипотеза о малости деформаций: по сравнению с размерами тела деформации настолько малы,  что не изменяют положения внешних сил, действующих на тело.

 Гипотеза об идеальной упругости: в заданных малых пределах деформирования все тела идеально упругие, т.е. деформации полностью исчезают после прекращения нагрузок.

Гипотеза плоских сечений: сечение плоское до деформирования остается плоским и после деформации.

 Закон Гука и гипотеза о малости деформаций дают возможность применять принцип суперпозиции (принцип независимости или сложения сил): деформации тела, вызванные действиями нескольких сил, равняются сумме деформаций, вызванных каждой силой.

 Прицип Сен-Венана: статически эквиваленте системы сил, действующие на малую, по сравнению с общими размерами тела, его часть, при достаточном отдалении от этой части вызывают одинаковые деформации тела.

 Принцип затвердения: тело, испытывающее деформирование, затвердело и к нему можно применять уравнения статики.

Внутренние силы. Метод сечений

 Внутренние силы – это силы механического взаимодействия между частичками материала, возникающие в процессе деформирования как реакции материала на внешнюю нагрузку.

 Для нахождения и определения внутренних сил применяют  метод сечений (РОЗУ), который сводится к следующим операциям:

• условно перерезаем тело на две части секущей плоскостью (Р -разрезаем);
• отбрасываем одну из частей (О - отбрасываем);
• заменяем влияние отброшенной части на оставленную внутренними силами (усилиями) (З - заменяем) ;
• из условий равновесия системы сил, действующих на оставшуюся часть, определяем внутренние силы (У – уравнения равновесия);

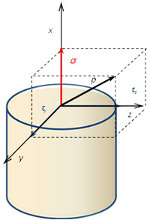
  В результате сечения стержня поперечным сечением, разорванные связи между частями заменяются внутренними силами, которые можно свести к главному вектору R и главному моменту М внутренних сил. При проектировании их на координатные оси получаем:
N – продольная (осевая) сила,
Qy – поперечная (перерезывающая) сила
Qz – поперечная (перерезывающая) сила
Mx – крутящий момент
My – изгибающий момент
Mz – изгибающий момент

 Если известны внешние силы, все шесть компонент внутренних сил могут быть найдены из уравнений равновесия

Напряжение

Нормальные напряжения, касательные напряжения. Полное напряжение.

 Определение зависимости между внешними силами, с одной стороны, и напряжением и деформацией, с другой, - основная задача сопротивлению материалов.

Растяжение и сжатие

 Растяжение или сжатие часто встречаются в элементах машин или сооружений (растяжение троса крана при подъеме груза; шатуна двигателя, штока цилиндров  в  подъёмно-транспортных машинах).

 Растяжение или сжатие – это случай нагружения стрежня, который характеризуется его удлинением или укорочением. Растяжение или сжатие вызывается силами, действующими вдоль оси стрежня.

 При растяжении стержень удлиняется, а его поперечные размеры уменьшаются. Изменение  начальной длины стрежня называют абсолютным удлинением при растяжении или абсолютным укорочением при сжатии. Отношение абсолютного удлинения (укорочение) к начальной длине стрежня  называется относительным удлинением.

В этом случае:

• ось стержня остается прямой линией,
• поперечные сечения стержня уменьшаются вдоль его оси параллельно самим себе (потому что поперечное сечение - это плоскость перпендикулярная оси стрежня, а ось - прямая линия);
• поперечные сечения остаются плоскими.

  Все волокна стрежня удлиняются на  одну и ту же величину и их относительные удлинения одинаковые.

 Разность соответствующих поперечных размеров после деформации и до нее называется абсолютной поперечной деформацией. 

 Отношение абсолютной поперечной деформации к соответствующему начальному размеру называется относительной поперечной деформацией.

 Между поперечной и продольной деформациями существует соотношение. Коэффициент Пуассона − безразмерная величина, находящаяся в пределах 0...0,5 (для стали 0,3).

 В поперечных сечениях  возникают нормальные напряжения. Зависимость напряжений от деформаций устанавливает закон Гука.

 В сечении стержня возникает один внутренний силовой фактор – продольная сила N. Продольная сила N является равнодействующей нормальных напряжений, которая численно равна алгебраической сумме всех внешних сил, действующих на одну из частей рассеченного стрежня и направленных вдоль его оси.

Формат: pdf

Язык: русский, украинский

Размер: 460 КВ

Представлен в полном объёме сопромат bcoreanda.com.