 Обзор
Обзор
Какое-либо кинематическое состояние тел, имеющих точку или ось вращения, можно описать моментом силы, характеризующим вращательный эффект действия силы.
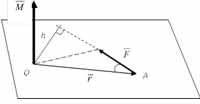
Момент силы относительно центра - это векторное произведение радиус – вектора точки приложения силы на вектор силы.
Плечо силы – кратчайшее расстояние от центра до линии действия силы (перпендикуляр из центра на линию действия силы).
Вектор направляется по правилу векторного произведения: момент силы относительно центра (точки) как вектор направлен перпендикулярно плоскости, в которой расположены сила и центр так, чтобы с его конца было видно, что сила пытается вращать тело вокруг центра против хода часовой стрелки.
Единицей измерения момента силы есть 1 [Hм]
Момент силы относительно центра в плоскости – алгебраическая величина, которая равняется произведению модуля силы на плечо относительно того же центра с учетом знака.
Знак момента силы зависит от направления, в котором сила пытается вращать вокруг центра:
- против хода часовой стрелки -„−” (отрицательный)
- по часовой стрелке -„+” (положительный);
-
Свойства момента силы относительно центра (точки).
- Модуль момента силы относительно точки равняется удвоенной площади треугольнику построенного на векторах.
- Момент силы относительно точки не изменяется при перенесении силы вдоль ее линии действия, поскольку неизменным остается плечо силы.
- Момент силы относительно центра (точки) равняется нулю , если:
- сила равняется нулю F = 0;
- плечо силы h = 0, т.е. линия действия силы проходит через центр.
Теорема Вариньона (о моменте равнодействующей).
Момент равнодействующей плоской системы сходящихся сил относительно какого-либо центра равняется алгебраической сумме моментов составляющих сил системы относительно того же центра.
Теория пар сил
Сложение двух параллельных сил, направленных в одну сторону.
Равнодействующая системы двух параллельных сил направленных в одну сторону равняется по модулю сумме модулей составляющих сил , параллельна им и направлена в том же направлении.
Линия действия равнодействующей проходит между точками приложения составляющих на расстояниях от этих точек, обратно пропорциональных к силам
Сложение двух параллельных сил, направленных в разные стороны (случай сил разных по модулю)
Равнодействующая двух параллельных, неравных по модулю, противоположно направленных сил параллельна им и направлена в направлении большей силы и по модулю равняется разности составляющих сил.
Линия действия равнодействующей проходит за пределами отрезка (со стороны большей силы), соединяющего точки их приложения, и отстоит от них на расстояния, обратно пропорциональные силам.
Пара сил – система двух параллельных, равных по модулю и противоположных по направлению сил, приложенных к абсолютно твердому телу.
Плечо пары сил – расстояние между линиями действия сил пары, т.е. длина перпендикуляра, проведенного из произвольной точки линии действия одной из сил пары на линию действия второй силы.
Плоскость действия пары сил – это плоскость, в которой расположены линии действий сил пары.
Действие пары сил сводится к вращательному движению, которое определяется моментом пары.
Моментом пары называется вектор с такими признаками:
- он перпендикулярен плоскости пары;
- направлен в ту сторону, откуда вращение, которое осуществляет пара, видно против часовой стрелки;
- его модуль равняется произведению модуля одной из сил пары на плечо пары с учетом знака
Знак момента пары сил:
- „+” – вращение против часовой стрелки
- „-„ – вращение по часовой стрелке
Момент пары сил равняется произведению модуля одной из сил пары на плечо пары.
Момент пары – свободный вектор – для него ни точка приложения, ни линия действия не обозначены, они могут быть произвольными.
Свойство момента пары сил: момент пары равняется моменту одной из сил относительно точки приложения второй силы.
Теоремы о паре сил
Теорема 1. Пара сил не имеет равнодействующей, т.е. пару сил нельзя заменить одной силой.
Теорема 2. Пара сил не является системой уравновешенных сил.
Следствие: пара сил, действующая на абсолютно твердое тело, старается вращать его.
Теорема 3. Сумма моментов сил пары относительно произвольного центра (точки) в пространстве является величиной неизменной и представляет собой вектор-момент этой пары.
Теорема 4. Сумма моментов сил, которые составляют пару, относительно произвольного центра в плоскости действия пары не зависит от центра и равняется произведению силы на плечо пары с учетом знака, т.е. самому моменту пары.
Теорема 5 - об эквивалентности пар. Пары сил, моменты которых равны численно и по знаку, являются эквивалентными. Т.е. пару сил можно заменить или уравновесить только другой эквивалентной парой сил.
Теорема 6 - об уравновешенности пары сил. Пара сил составляет уравновешенную систему сил тогда и только тогда, когда момент пары равняется нулю.
Теорема 7 - о возможностях перемещения пары сил в плоскости ее действия. Пара сил, полученная перемещениям пары в любое место в плоскости ее действия, эквивалентна предоставленной паре.
Теорема 8 - о добавлении пар сил в плоскости. Момент пары, эквивалентной предоставленной системе пар в плоскости, равняется алгебраической сумме моментов составляющих пар. Т.е. для сложения пар сил необходимо сложить их моменты.
Условия равновесия системы пар сил.
Пары сил в плоскости уравновешиваются в том случае, если алгебраическая сумма их моментов равняется нулю.
Язык: русский, украинский
Размер: 500 КВ
Пример решения задачи