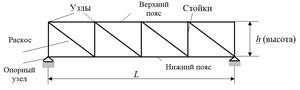
 Фермой называется геометрически неизменная шарнирно-стержневая конструкция.
Фермой называется геометрически неизменная шарнирно-стержневая конструкция.
Ферма называется плоской, если все стержни фермы лежат в одной плоскости.
Определенность или устойчивость фермы отображает зависимость количества узлов и стержней фермы:
Ферма определена, устойчивая
K = 2N - 3 ;
Ферма является неопределенной, имеет лишние стержни
K > 2N - 3 ;
Ферма неустойчивая и является механизмом
K < 2N - 3 .
При расчете фермы трением в узлах и весом стрежней пренебрегают, или распределяют вес стержней по узлам.
Все внешние нагрузки (силы) к ферме прикладывают только в узлах, поэтому все стержни фермы испытывают или сжатие, или растяжение.
Расчет фермы сводится к определению опорных реакций и усилий в ее стержнях.
Для определения реакций опор составляют и решают три уравнение равновесия, считая ферму абсолютно твердым телом под действием известных внешних нагрузок (активных сил) и неизвестных реакций опор (реактивных сил).
Для определения усилий в стержнях ферм существует 2 метода.
Метод вырезания узлов
Метод вырезывания узлов заключается в том, что мысленно вырезают узлы фермы, прикладывая к ним соответствующие внешние силы, реакций опор и реакции стрежней, и составляют уравнение равновесия сил, приложенных к каждому узлу.
Вырезается узел с 2-мя неизвестными усилиями, так как в каждом узле составляется сходящаяся система сил, соответственно, составляют два уравнение равновесия
Условно допускают, что все стержни растянуты, т.е. реакции стержней направлены от узлов.
Метод Риттера
Метод Риттера заключается в том, что ферму разделяют на две части сечением, проходящим через три стрежня, в которых нужно определить усилия, и рассматривают равновесие одной из частей. Действие отброшенной части заменяют соответствующими силами, которые направляют вдоль разрезанных стержней от узлов.
Потом составляют уравнение равновесия для плоской произвольной системы сил
Точка Риттера (центр моментов) – это такая точка для каждого с трех рассеченных стрежней, в которой пересекаются два других стержня данного сечения, например точка К – точка Риттера для определения усилия в стержне 6.
Относительно точки Риттера составляют уравнение суммы моментов выбранной части фермы.
В случае, если стержни не имеют точки пересечения, т.е. являются параллельными, составляется уравнение равновесия в виде суммы проекций всех сил выбранной части фермы на ось, перпендикулярную этим стержням.
Размер: 200КВ
Язык: русский, украинский