 Механическая система
Механическая система
Механической системой материальных точек или тел называется такая их совокупность, в которой положение и движение каждой точки (или тела) зависит от положения и движения остальных.
Материальное тело рассматривается, как система материальных точек (частиц), которые образуют это тело.
Классификация сил, действующих на механическую систему.
Внешними называют такие силы, которые действуют на точки или тела механической системы со стороны точек или тел, не принадлежащих данной системе.
Внутренними , называют такие силы, которые действуют на точки или тела механической системы со стороны точек или тел той же системы, т.е. с которыми точки или тела данной системы взаимодействуют между собой.
Одни и те же силы могут быть как внутренними, так и внешними, в зависимости от рассматриваемой системы.
Внешние и внутренние силы системы, в свою очередь могут быть активными и реактивными.
Свойства внутренних сил.
- Геометрическая сумма (главный вектор) всех внутренних сил системы равен нулю
- Сумма моментов (главный момент) всех внутренних сил системы относительно какого-нибудь центра или оси равен нулю
Масса системы. Центр масс
Масса системы равняется алгебраической сумме масс всех точек или тел системы.
В однородном поле силы тяжести, для которого , вес любой частицы тела пропорционален ее массе. Поэтому распределение масс в теле можно определить по положению его центра тяжести – геометрической точки С, координаты которой называют центром масс или центром инерции механической системы
Дифференциальные уравнения движения механической системы
Теорема о движении центра масс механической системы
Центр масс механической системы движется как материальная точка, масса которой равна массе системы, и к которой приложены все внешние силы, действующие на систему.
Выводы:
- Механическую систему или твердое тело можно рассматривать как материальную точку в зависимости от характера ее движения, а не от ее размеров.
- Внутренние силы не учитываются теоремой о движении центра масс.
Теорема о движении центра масс не характеризует вращательное движение механической системы, а только поступательное.
Закон о сохранении движения центра масс системы
- Если сумма внешних сил (главный вектор) постоянно равен нулю, то центр масс механической системы находится в покое или движется равномерно и прямолинейно.
- Если сумма проекций всех внешних сил на какую-нибудь ось равна нулю, то проекция скорости центра масс системы на эту же ось величина постоянная.
Примеры применения теоремы о движении центра масс
Теорема о движении центра масс является одной из основных теорем динамика, которая объясняет многие явления.
Движение транспортного средства по горизонтальному пути
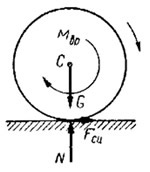
При движении локомотива или автомобиля по горизонтальной поверхности перемещение его центра масс происходит под действием сил сцепления, приложенных к ведущим колесам в точках соприкасания их с поверхностью рельсов или дороги. Эти силы направлены в сторону движения и являются внешними.
Со стороны двигателя к ведущему колесу приложен вращающий момент, которому со стороны дороги препятствует сила сцепления, заставляющая колесо катиться, а транспортное средство двигаться в ту сторону, куда направлена эта сила.
Вращающий момент относится к внутренним силам, и вызвать движение центра масс локомотива или автомобиля не может. Этот момент только вызывает появление внешних сил сцепления. На абсолютно гладких рельсах под действием вращающего момента колеса транспортного средства будет буксовать.
Торможение также вызывается внешними силами, приложенными к колесам со стороны дороги. К ведомому колесу, которое не связано с двигателем, приложена сила давления на ось. При торможении величина силы сцепления, направленной противоположно движению и препятствующей скольжению колеса, возрастает. В результате этого движение транспортного средства замедляется. Силы взаимодействия между тормозными колодками и колесом – внутренние, и не приводят к торможению, а являются причиной увеличения внешней силы сцепления. При буксовании сила сцепления превращается в силу трения скольжения.
Отдача при стрельбе
Возникающие при выстреле внутренние силы взрыва не могут привести к движению центра масс системы орудие – снаряд. При горизонтальном вылете снаряда свободно стоящее орудие откатывается в противоположную сторону, так как при отсутствии внешних сил, направленных горизонтально, центр масс системы орудие-снаряд не может перемещаться горизонтально. В действительности внешней горизонтальной силой является реакция шероховатой поверхности, но она мала и практически не влияет на это явление.
Формат: pdf.
Язык: русский, украинский
Размер: 540КВ